Hi! I am Kewei Lian (连可为). I am currently a PhD student at School of Computing, National University of Singapore (NUS), advised by Prof. Anji Liu.

I obtained my B.S. degree in Computer Science from Peking University (PKU) in 2025. I was in the team of CraftJavis, advised by Prof. Yitao Liang. I also worked with Prof Di He on the topic of NLP during my undergraduate studies.

Research interests:

• Machine Learning Architecture and Interpretablity
• Designing Memory for Models and Agents

Publications

Below is a list of selected publications. Please refer to my Google Scholar for the full list of publications.

Toward Memory-Aided World Models: Benchmarking via Spatial Consistency

Kewei Lian, Shaofei Cai, Yilun Du, Yitao Liang

Arxiv Preprint / Paper / Code

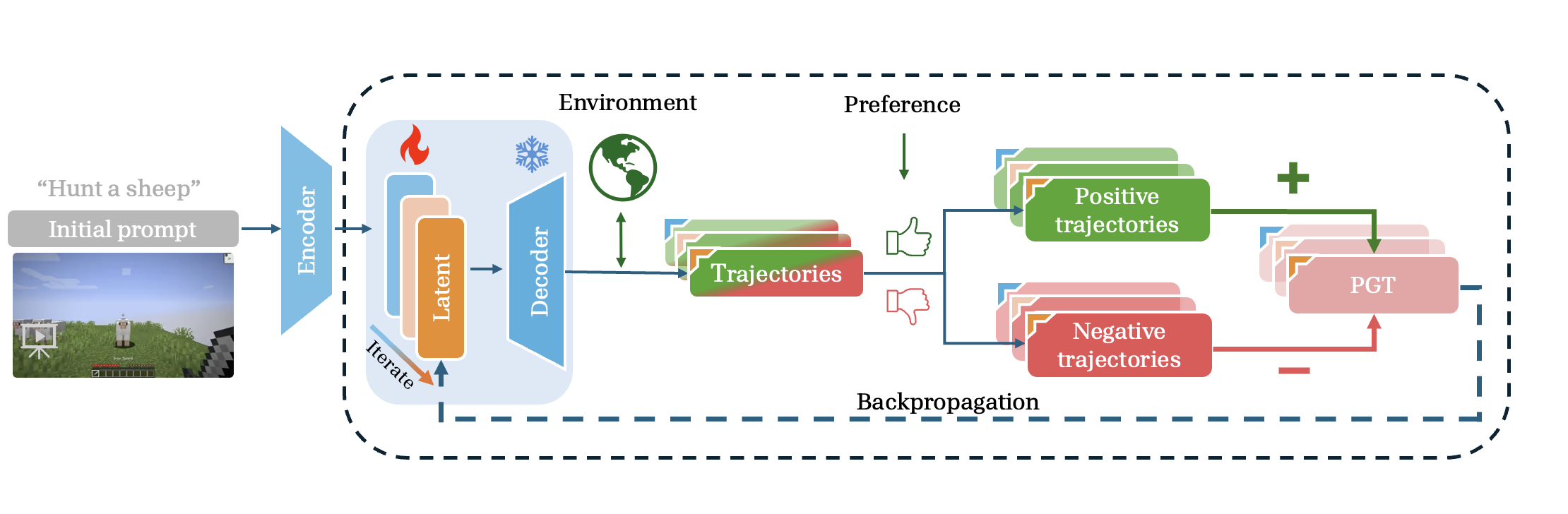
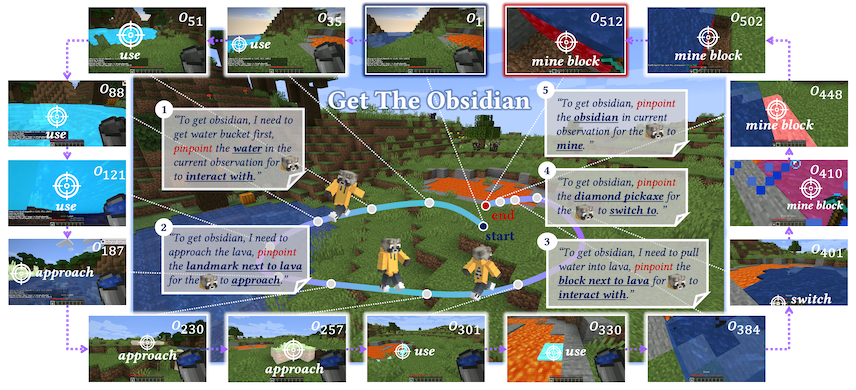
Optimizing latent goal by learning from trajectory preference

Guangyu Zhao*, Kewei Lian*, Haowei Lin, Haobo Fu, Qiang Fu, Shaofei Cai, Zihao Wang, Yitao Liang

Arxiv Preprint / Paper

Optimizing latent goal by learning from trajectory preference

Shaofei Cai, Zihao Wang, Kewei Lian, Zhancun Mu, Xiaojian Ma, Anji Liu, Yitao Liang

CVPR 2025 / Website / Paper / Code

Others

In my spare time, I enjoy swimming, hiking, and playing baseball~

I’m always happy to chat! Feel free to reach out to me via email for anything!